BiBitR enters the fray!
Ewoud De Troyer, University of Hasselt (CenStat)
Introduction
The latest patch of the BiclustGUI includes the implementation of BiBitR, a simple R wrapper which directly calls the original Java code for applying the BiBit algorithm after which the output is transformed to a Biclust S4 class object. The original Java code can be found at http://eps.upo.es/bigs/BiBit.html by Domingo S. Rodriguez-Baena, Antonia J. Perez-Pulido and Jesus S. Aguilar-Ruiz.
More details about the BiBit algorithm can be found in:
Installation Instructions
setRepositories(ind=c(1:5))
install.packages("RcmdrPlugin.BiclustGUI")
BiBit with Noise Allowance
The BiBit algorithm is a biclustering method for binary data. By converting the binary data to bit words, it is a very efficient algorithm in finding perfect biclusters (all 1’s in the BC). The algorithm was slightly adapted in the BiBitR R package in order to also allow some noise in the discovered biclusters.
The general steps of the BiBit algorithm go as following:
- Binary data is encoded in bit words.
- Take a pair of rows as your starting point.
- Find the maximal overlap of 1’s between these two rows and save this as a pattern/motif. You now have a bicluster of 2 rows and N columns in which N is the number of 1’s in the motif.
- Check all remaining rows if they match this motif, however allow a specific amount of 0’s in this matching as defined by the noise parameter. Those rows that match completely or those within the allowed noise range are added to bicluster.
- Go back to Step 2 and repeat for all possible row pairs.
Biclusters are only saved if they satisfy the Minimum Row Size and Minimum Column Size parameter settings of the biclusters and if the bicluster is not already contained completely within another bicluster. What you will end up with are biclusters not only consisting out of 1’s, but biclusters in which 2 rows (the starting pair) are all 1’s and in which the other rows could contain 0’s (depending on the Noise parameter).
For larger data, in order to avoid too many discovered biclusters as well as overhead issues in the algorithm, it is advised to put the Minimum Row/Column Size parameter sufficiently high.
Note: The BiBitR package also contains a procedure to add extra columns to the discovered BiBit BC’s. This was not included in the GUI, however more information can be found in the bibit2 documentation of the BiBitR R package.
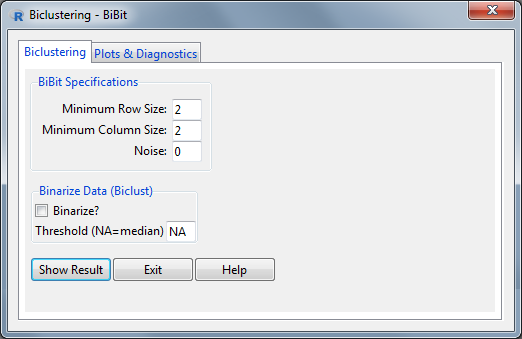
BiBit Window
The Noise parameter determines the amount of zero’s allowed in the bicluster (i.e. in the extra added rows to the starting row pair) and can take on the following values:
- Noise=0: No noise allowed. This gives the same result as using the original BiBit algorithm.
- 0<Noise<1:
The noise parameter will be a noise percentage. The number of allowed 0’s in a (extra) row in the bicluster will depend on the column size of the bicluster. More specifically
zeros_allowed = ceiling(noise * columnsize). For example for Noise=0.10 and a bicluster column size of 5, the number of allowed 0’s would be 1. - Noise>=1: The noise parameter will be the number of allowed 0’s in a (extra) row in the bicluster independent from the column size of the bicluster. In this noise option. The noise parameter should be an integer.
The second Plots & Diagnostics tab contains the same graphs and diagnostics as the other biclust methods in the GUI. (Only the Summary button has been switched out for a Top Maximum BC button.)
Using BiBit to find provided patterns
Normally you would apply BiBit (with/without noise) directly on the binary data. However due to the nature of the algorithm, namely starting an exhaustive search from each row-pair, it is also possible to look for specific patterns of interest therefore decreasing the solution space and compation time. This more “directed” or “pattern-driven” version of the BiBit algorithm is implemented in the following Bibit Patterns Window. It allows the user to only look for one or multiple full or sub patterns in their data.
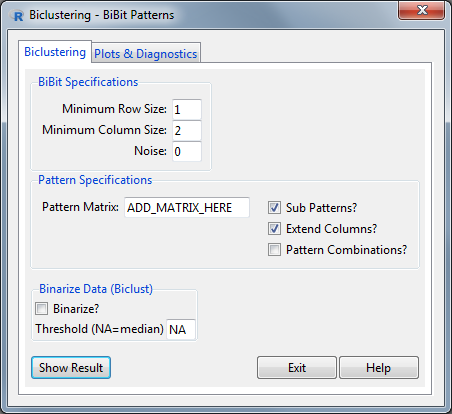
BiBit Patterns Window
The window contains the same BiBit Parameters and Binarization option as before. Additionally now also some parameters have to be set for the pattern(s) of interest. In the Pattern Matrix field, the name of a loaded or created matrix must be provided. This matrix is a Number of Patterns X Number of Data Columns matrix in which each row corresponds with a given pattern of interest.
Three types of Biclusters can be discovered based on the provided patterns:
- Full Pattern: Bicluster which overlaps completely (within allowed noise levels) with the provided pattern. The column size of this bicluster is always equal to the number of 1’s in the pattern.
- Sub Pattern: Biclusters which overlap with a part of the provided pattern within allowed noise levels.
- Extended: Using the resulting biclusters from the full and sub patterns, other columns will be attempted to be added to the biclusters while keeping the noise as low as possible (the number of rows in the BC stays constant). Naturally the articially added pattern rows will not be taken into account with the noise levels as they are 0 in each other column. The question which is attempted to be answered here is “Do the rows, which overlap partly or fully with the given pattern, have other similarities outside the given pattern?”
The 3 checkboxes in this window determine if Sub Patterns should be discovered (unchecked means decreased computation time), if the Extend Columns procedure should be applied and if Combinations of Patterns should also be investigated.
The Plots & Diagnostics Tab contains a Summary button which prints the indices and dimensions of the biclusters which fall in the 3 types described above. Finally in this tab it is also possible to print any bicluster together with its given pattern.
Shiny Application
The BiBit algorithm (with noise allowance) has also been included in a small new update for the Shiny Application. The Standalone Version is also available here.
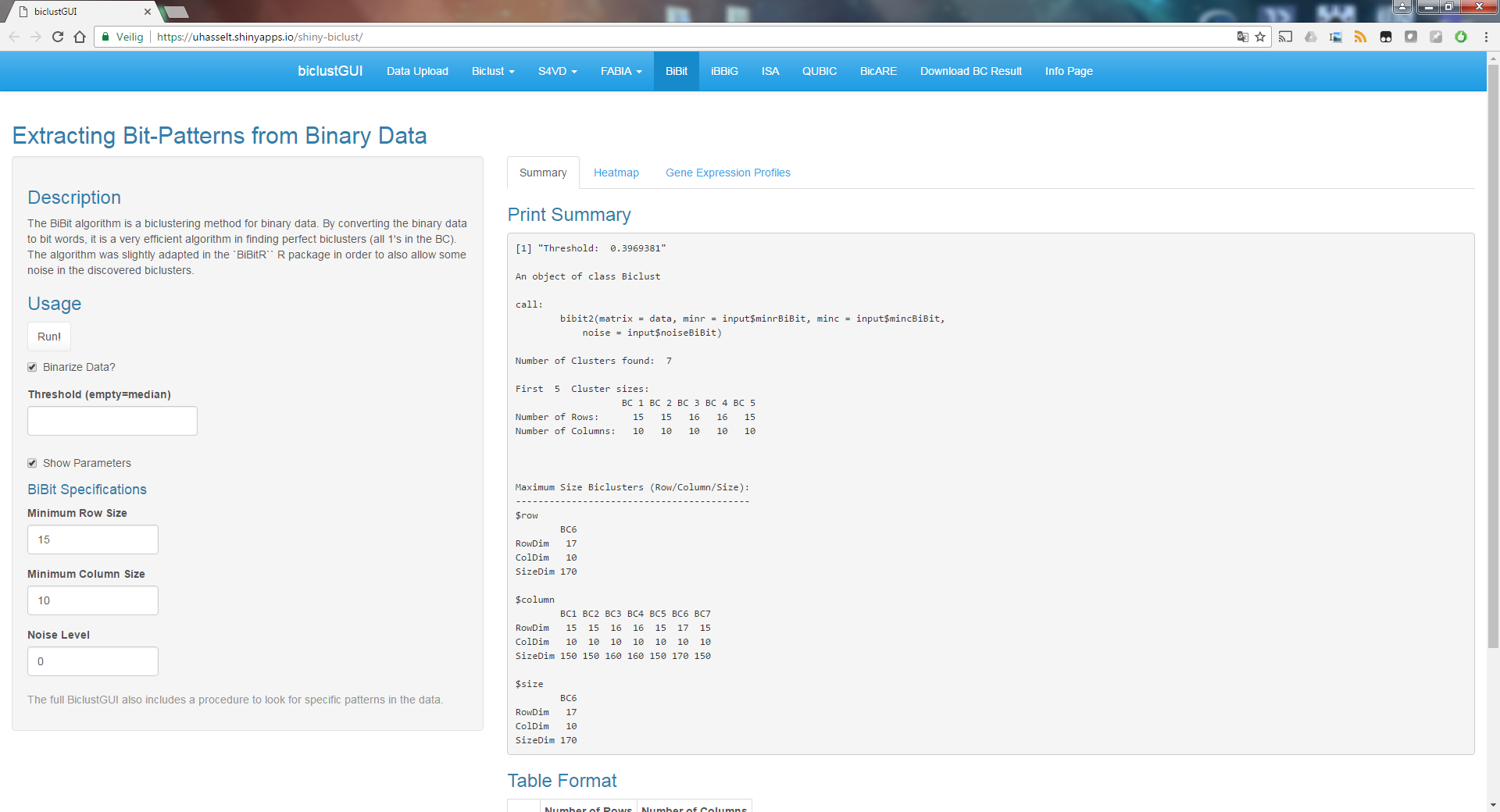
BiBit Patterns Window
Re-implementation of superbiclust
A central issue of biclustering is its stability which can highly influence the ability to interpret the results of a biclustering analysis. The stability can be affected by initialisation, parameter settings and perturbations such as random noise. Shi et al. (2010) introduced a novel procedure for obtaining robust biclusters from a set of initial values which is exactly what the superbiclust R package will accomplish.
The superbiclust package had already been implemented in the GUI, but it has now been made easier to repeat a similar biclustering algorithm multiple times and feed it into the superbiclust framework.
A detailed guide on the superbiclust window can be found in the Vignette.
Contact
Please direct any questions/suggestions/bugs to ewoud.detroyer[at]uhasselt.be.
We are happy to take any feedback!